Приколы, юмор, анекдоты, фото, картинки, все самое смешное и интересное только здесь!
Не стало «отца фракталов» Бенуа Мандельброта

Бенуа Мандельброт — родился в Польше, учился во Франции, работал во Франции, Швейцарии и США, умер 14 октября 2010 года.
Причина смерти— рак поджелудочной железы, место— больница для умирающих, хоспис, в Кембридже (не в том, который в Великобритании, а том, что в штате Массачусетс). Дата— 14 октября, сообщения в зарубежной прессе появились лишь три дня спустя после того, как «отца фракталов» не стало.
Кто он?
Однозначно говорить о национальной принадлежности ученого сложно. Родился он в Варшаве, в семье литовских евреев— что и определило их переезд во Францию в 1936 году. С началом войны пришлось переехать из Парижа в Тюль, но потом Бенуа снова вернулся в Париж, выбрав Политехническое училище для получения математического образования. Потом была учеба в США, потом снова Париж, щвейцарская Женева и с 1958 года— лаборатории компании IBM

Тюль, городок с населением чуть больше 15 тысяч человек. Название не случайно напоминает ткань, из которой шьют полупрозрачные шторы: именно тут ее и начали делать
Исследовательский центр этой крупнейшей компании тогда был одним из наиболее сильных научных центров при коммерческих корпорациях и в нем Мандельброт сделал то открытие, которое принесло ему всемирную известность: фрактальное множество, получившее впоследствии его имя. И хотя ученый занимался многими другими вещами, у большинства нематематиков он ассоциируется именно с самоподобным объектом, который можно бесконечно увеличивать и получать все новые и новые красочные картинки
Детали
В школе Бенуа было неинтересно. Но у него оказалось великолепное пространственное мышление и желание исследовать самые разные проблемы: позже, при работе в IBM, он занимался не столько конкретными прикладными работами, сколько общими исследованиями. От аэродинамики до физиологии и от теории игр до фондовых рынков. Впрочем, отметим что Мандельброт имел чувство меры, его широта интересов не имела ничего общего с "(external-link) сомнительными достижениями некоторых одиозных фигур нашего времени.
Фракталы
Фрактал— это фигура, отдельные части которой повторяют весь рисунок в целом. Если увеличить произвольный фрагмент фрактала, то он покажет схожую с цельной фигурой структуру, с теми же деталями, но меньшего масштаба. А если увеличить и их, то все повторится, фракталы как математические объекты можно увеличивать сколь угодно сильно и получать при этом новые изображения.
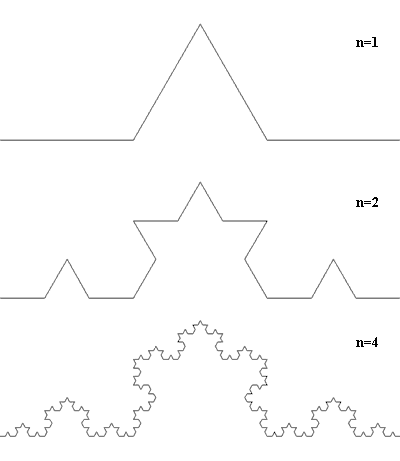
Кривая Коха. Алгоритм построения ясен из рисунка (только надо уточнить, что добавление меньших треугольников производится бесконечное число раз!); примечательна тем, что к идеальной кривой Коха нигде нельзя провести касательную.
Фракталы были известны до Мандельброта: помимо кривой Коха стоит отметить так называемое множество Жюлиа, названное так по имени Гастона Жюлиа, специалиста в области комплексных чисел и французского математика начала XX века. Но именно Мандельброт ввел в обиход термин «фрактал» и, сверх того, ему принадлежит целый ряд попыток рассмотреть эти объекты не просто как математический курьез— при помощи фракталов ученый даже предложил объяснение парадокса Ольберса.
Космологическая загадка
Если Вселенная бесконечна, то тогда любая линия, проведенная из глаза в небо, рано или поздно наткнется на звезду. Почему небо черное? Астрономы сейчас знают: Вселенная не бесконечна и расширяется, это снимает названный в честь Генриха Вильгельма Маттеуса Ольберса (немецкий астроном XVIII-XIX веков, открыл астероиды Весту и Палладу) парадокс.
Мандельброт показал, что решение загадки можно получить и без Большого взрыва, если принять что звезды расположены на небе по фрактальному принципу. Впрочем, это не объясняло другое— например сдвиг спектра дальних звезд в сторону красного света и реликтовое излучение.
Знаменитое множество Мандельброта было описано в 1905 году Пьером Фату, но увидеть его ученый начала столетия не мог: вручную сделать необходимое число вычислений было физически невозможно. Для этого потребовались компьютеры— которыми воспользовался Бенуа Мандельброт для изучения уже описанного, но еще толком не исследованного объекта.
Множество Мандельброта — лучше один раз увидеть в движении, чем сто раз на статичных картинках
ТФКП в трех абзацах
Область математики, которая породила фракталы, изучается в институтах в рамках дисциплины под названием «теория функция комплексных переменных». На нее уходит не меньше семестра, однако для понимания сути открытия Мандельброта хватит и двух абзацев

Комплексные числа часто показывают как точки на плоскости: по одной оси отложена та часть, что без мнимой единицы (ее еще называют действительной, ось Re), по другой — та, что с мнимой единицей i (мнимая часть, ось Im).
Прежде всего, математики используют не только обычные числа, но и комплексные, состоящие из двух частей. Комплексное число выглядит, например, так: {4 + 5i}. Или {-56,54 + 2,0034i}. Или, в общем виде, {x + iy}. Буква i обозначает так называемую мнимую единицу, которая при возведении в квадрат дает— 1 и это в комплексных числах самое сложное— ведь школьная программа по математике утверждает, что квадратных корней из отрицательных чисел не бывает. Действительно, не бывает, но лишь если говорить об обычных числах— мнимая единица это совсем другое дело!
Комплексные числа можно складывать:
(a + bi) + (c + di) = (a + c) + (b + d)i
и умножать:
(a + bi)*(c + di) = ac + bic + adi + bidi = ac + (bc+ad)i + bd(-1) = ac— bd + (bc+ad)i
— что, конечно, чуть более громоздко, чем действия с обычными числами, но при желании можно и возвести комплексное число в квадрат. Что как раз необходимо для алгоритма, который рисует поразительные по красоте изображения множества Мандельброта.
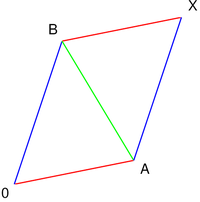
Комплексное число X (здесь оно показано как точка на комплексной плоскости) является суммой двух комплексных чисел A и B. Сложение происходит в точности так же, как складываются обычные векторы в школьной геометрии.
Происходит это следующим образом— берется произвольное комплексное число z = x+iy, возводится в квадрат и складывается с еще одним произвольным, но все время одинаковым комплексным числом, некоторой константой. Полученный результат опять возводится в квадрат, опять складывается с той же константой… и так до тех пор, пока не станет ясно, что эти числа будут неизбежно увеличиваться вплоть до бесконечности.
От алгоритма к картинке
Если возвести обычное число в квадрат, сложить с другим числом и снова возвести в квадрат— что получится? Если взять в качестве чисел 0,5 и 0,05— то с каждым шагом мы будем приближаться к нулю. Если же взять 2 и 3— то, напротив, начнем двигаться в бесконечность. Если число комплексное, то какие-то точки комплексной плоскости (плоскости с двумя осями для x и для iy) точно так же дадут выход на бесконечность… вот только какие?
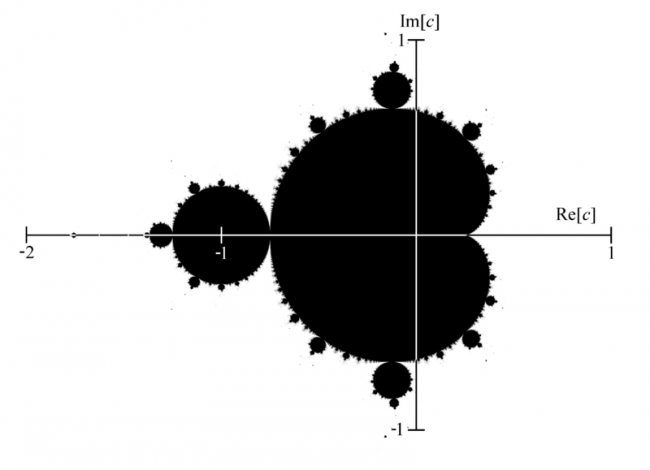
Множество Мандельброта. Здесь оно показано черно-белым: для черных точек алгоритм построения множества никогда не даст бесконечного результата. Есть и цветные варианты: там цвет кодирует число шагов, за которые последовательное возведение в квадрат и сложение комплексных числе дает некоторое определенное значение.
Множеством Мандельброта являются все те точки, для которых применение указанного алгоритма не дает бесконечности в итоге. И если начать его рисовать, закрашивая такие точки одним цветом— получится очень странная фигура.
Множества, определенные по другим законам (скажем, «все точки {x, y}, для которых {x+iy} меньше комплексного числа z») имеют гладкие и ровные границы— а вот множество Мандельброта, равно как и множество Жюлиа, также заданное через манипуляции с комплексными числами, оказывается фракталом.
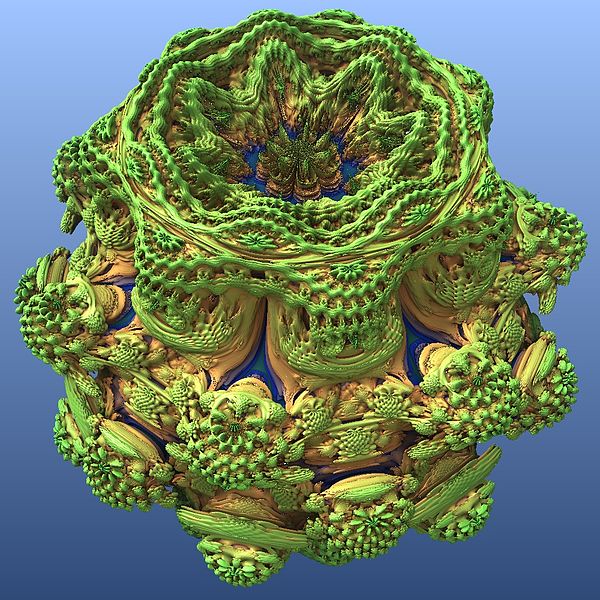
Эта жутковатая конструкция получается, если ввести в рассмотрение комплексные числа не с двумя, а тремя частями, к x+iy добавили еще один компонент. Показанное множество носит полуофициальное название «лампочки Мандельброта».
От картинки к практике
Сам по себе эффект фрактальности множества, которое задано сравнительно простым алгоритмом, поразителен. Если кривая Коха или снежинка Серпинского более-менее очевидна, то вот причудливые формы множества Мандельброта поражают воображение.
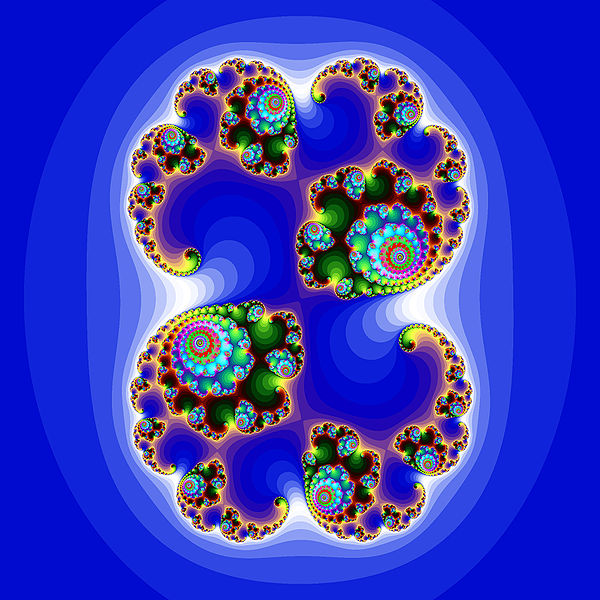
Множество Жюлиа в цвете — множество Мандельброта является частным случаем этой структуры.
Изображения, полученные ученым и описанные в его книге 1975 года «Les Objets Fractals: Forme, Hasard et Dimension» («Фрактальные объекты: форма, случайность и размерность») наталкивают на мысль о том, что за этой сложностью определенно что-то кроется. Правила, по которым формируются кроны деревьев или сеть кровеносных сосудов— сам Мандельброт пытался найти фракталам применения за пределами абстрактной математики.

Каждая картинка является увеличением предыдущей. Слева направо, начиная с верхнего ряда.
Так, ученый смог показать, что долговременные колебания цен на хлопок подобны тем, которые характерны для сравнительно небольших промежутков времени. Иными словами, поведение рынка может описываться чем-то вроде фракталов! И на сходстве многих реальных объектов и явлений с математическими идеями применение фракталов не исчерпывается: много позже, уже на рубеже XXI века, фрактальные структуры стали рисовать в компьютерной анимации. Огонь, нарисованный по схожим правилам, будет колебаться не повторяя одну и ту же последовательность кадров, а ведя себя почти как настоящее пламя, точно так же можно создавать рисунок ряби или разводов на воде. Область применения разработок Мандельброта простирается от анализа фондового рынка до компьютерных игр.
Фракталами можно просто любоваться — они стали основой для ряда красивых клипов. Это уже не столько математика, сколько искусство. Кстати, при изучении музыки как звуковых колебаний ученые находили… правильно, фрактальные структуры.
Комментарии (0)
RSS свернуть / развернутьТолько зарегистрированные и авторизованные пользователи могут оставлять комментарии.